いつの間にか「速度算」という名前になっていますが、私などは「旅人算」の方が馴染みがあります。出会ったり、追いついたりする人・物の距離、時間、速さを求める問題です。
SPI速度算(旅人算)の例題
<例題1>
Pは分速60m、Sは分速70mで歩く。ある地点から2人が同時に反対方向に向かって歩いた。15分後、2人の距離はどのくらい離れるか。
A 130m B 150m C 400m D 950m
E 1950m F 2050m G 2100m H A~Gのいずれでもない
<例題2>
Pは分速60m、Sは分速70mで歩く。ある地点から2人が同時に同じ方向に向かって歩いた。20分後、2人の距離はどのくらい離れるか。
A 100m B 130m C 150m D 180m
E 190m F 200m G 210m H A~Gのいずれでもない
<例題3>
Pは分速60m、Sは分速70mで歩く。2人は1560m離れた所から同時に向かい合って出発した。何分後に2人は出会うか。
A 10分後 B 12分後 C 13分後 D 15分後
E 16分後 F 18分後 G 20分後 H A~Gのいずれでもない
<例題4>
Pは分速60mで家を出発した。30分後、Sは自転車に乗って分速180mでPを追いかけた。Pが出発してから何分後にSはPに追いつくか。
A 10分後 B 20分後 C 25分後 D 30分後
E 35分後 F 40分後 G 45分後 H A~Gのいずれでもない
<例題5>
Pは分速60m、Sは分速70mで歩く。周囲360mの池を2人が同じ所から同じ方向に歩きだした。何分後にSはPに追いつくか。
A 36分後 B 40分後 C 42分後 D 46分後
E 50分後 F 56分後 G 60分後 H A~Gのいずれでもない
例題の解答・解説
解答・解説を見るには、「≫ 例題の解答・解説を見る」をクリック(タップ)してください。
≫ 例題の解答・解説を見る
<例題1>
答え:E
2人は1分間に(60+70)m離れるので、
(60+70)×15=1950
<例題2>
答え:F
2人は1分間に(70-60)m離れるので、
(70-60)×20=200
<例題3>
答え:B
2人は1分間に(60+70)m近づくので、
1560÷(60+70)=12
<例題4>
答え:G
30分間にPが進んだ距離は、60×30=1800(m)
1800mの距離をPとSの速さの差で縮めることになる。
1800÷(180-60)=15
Sは30分後に出発しているので、
30+15=45(分)
<例題5>
答え:A
周囲の長さをPとSが離れている距離と考える。
この距離をSはPとSの速さの差で縮めていく。
360÷(70-60)=36
≫ 例題の解答・解説を隠す
SPI速度算(旅人算)の練習問題
高校生は1~7の問題ができれば合格です。
2番の問題の数値に誤りがありましたので訂正しました。
4番の解答が間違っていましたので訂正しました。D → F
紙に印刷したい方は、下記のPDF(sokudozan.pdf)ファイルをご利用ください。
この練習問題のプリントはこちら>>sokudozan.pdf
1.Pは時速3.6km、Sは時速4.2kmで歩く。ある地点から2人が同時に反対方向に向かって歩いた。15分後、2人の距離はどのくらい離れるか。
A 130m B 150m C 400m D 950m
E 1950m F 2050m G 2100m H A~Gのいずれでもない
2.Pは時速3.3km、Sは時速4.5kmで歩く。ある地点から2人が同時に同じ方向に向かって歩いた。20分後、2人の距離はどのくらい離れるか。
A 120m B 180m C 200m D 280m
E 300m F 400m G 420m H A~Gのいずれでもない
3.分速60mのPと分速70mのSが、39km離れた所から同時に向かい合って出発した。何時間で2人は出会うか。
A 2時間 B 3時間 C 4時間 D 5時間
E 6時間 F 7時間 G 8時間 H A~Gのいずれでもない
4.兄は家から学校まで分速60mで歩き、所要時間は30分である。弟は家から学校まで40分かかる。弟の速さは分速何mか。
A 20m B 25m C 30m D 35m
E 40m F 45m G 50m H A~Gのいずれでもない
5.弟は家を出て分速55mで歩いている。弟が家を出て6分後に、兄は家を出て分速65mで弟を追いかけた。兄は家を出てから何分後に弟に追いつくか。
A 30分後 B 33分後 C 35分後 D 36分後
E 39分後 F 40分後 G 42分後 H A~Gのいずれでもない
6.周囲1515mの池がある。姉が分速75mで出発してから4分後に、同じ地点から反対方向に妹が分速60mで歩き出した。2人が出会うのは姉が出発してから何分後か。
A 9分後 B 10分後 C 12分後 D 13分後
E 15分後 F 20分後 G 23分後 H A~Gのいずれでもない
7.周囲976mの池がある。ある地点から姉と妹は同時に反対方向に歩き出した。姉が分速68mで歩くとすると、8分後に2人が出会うには妹は分速何mで歩かなければならないか。
A 54m B 56m C 60m D 62m
E 68m F 70m G 72m H A~Gのいずれでもない
8.P地点からS地点まで歩くのに、分速50mと分速65mとではかかる時間に6分の差ができる。P地点とS地点の間の距離は何mか。
A 300m B 390m C 460m D 680m
E 880m F 1250m G 1300m H A~Gのいずれでもない
9.弟は自転車に乗って家を出発した。弟が出発して8分後、兄は自転車に乗って弟を追った。弟は2km行ったところで忘れ物に気づき引き返すと、途中で兄に出会った。2人が出会ったのは、兄が出発してから何分後か。弟の速さは時速9km、兄の速さは時速12kmであった。
A 6分後 B 7分後 C 8分後 D 9分後
E 10分後 F 12分後 G 15分後 H A~Gのいずれでもない
10.家から駅までいつも分速60mで歩くが、今日は分速90mで走って駅まで向かった。途中で1分間休憩したが、それでもいつもより4分早く駅に着いた。家から駅まで何mあるか。
A 500m B 560m C 600m D 650m
E 680m F 720m G 900m H A~Gのいずれでもない
練習問題の解答・解説
解答・解説を見るには、「≫ 練習問題の解答・解説を見る」をクリック(タップ)してください。
≫ 練習問題の解答・解説を見る
1.E
時速3.6km=分速60m
時速4.2km=分速70m
(60+70)×15=1950(m)
2.F
時速3.3km=分速55m
時速4.5km=分速75m
(75-55)×20=400(m)
3.D
分速60mは、時速60×60÷1000=3.6km
分速70mは、時速70×60÷1000=4.2km
39÷(3.6+4.2)=5(時間)
4.F
家から学校までの距離は、60×30=1800(m)
1800÷40=45(m)
5.B
弟は6分間に55×6=330m歩いている。
兄は330mを2人の速さの差で縮めていくので、
330÷(65-55)=33(分後)
(注)問いは弟が出発してからではない。
6.D
姉は4分間で、75×4=300m進んでいる。
残りの1515-300=1215mを同じ地点から同時に反対方向に出発したと考えると、1215÷(75+60)=9分で出会うことになる。
姉が出発してからなので、4+9=13(分後)
7.A
姉は8分間で、68×8=544m歩く。
残りの976-544=432mを妹が歩くには、分速432÷8=54mの速さが必要である。
8.G
分速50mの人がS地点に到着したとき、分速65mの人は6分先まで行っていると考えてみる。
距離にすると、分速65mの人は、65×6=390m先まで行っていることになる。
390mの差は分速の差で生じているので、390mを分速の差で割ると
390÷(65-50)=26分
分速50mの人がS地点に到着したとき、どちらも26分間歩いたことになる。
よって、50×26=1300(m)
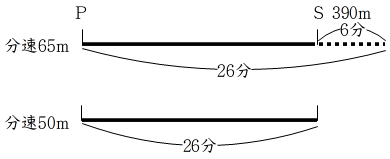
<別解>
分速65mの人がS地点に到着したとき、分速50mの人はS地点まであと6分かかると考えてみる。
距離にすると、分速50mの人は、あと50×6=300m歩かなければならない。
300mの差は分速の差で生じているので、300mを分速の差で割ると、
300÷(65-50)=20分
分速65mの人がS地点に到着したとき、どちらも20分間歩いたことになる。
よって、65×20=1300(m)
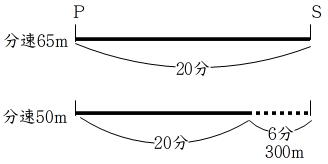
9.C
時速9km=分速150m
時速12km=分速200m
弟が8分間で進んだ距離は、150×8=1200m
兄が出発してから弟と出会うまでに2人が進んだ距離の和は、
2000×2-1200=2800(m)
2800mを2人の速さの和で進むのにかかる時間は、
2800÷(150+200)=8(分)
10.G
途中で休憩していようが、かかった時間の差は、1+4=5分である。
5分間分速90mで走ると、90×5=450m進む。
450mを分速の差で割ると、家から駅までかかった時間がでる。
450÷(90-60)=15(分)
60×15=900(m)
考え方は8番の問題と同じです。
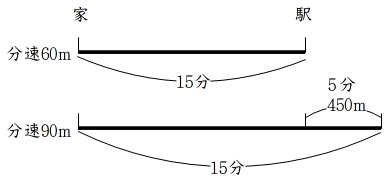
分速60mの人と分速90mの人が、同時に同じ家から出発すると、分速60mの人が駅に着いたときには、分速90mの人はそれより450m先にいると考える。
450mの差は、速さの差なので、距離を速さの差で割ることにより、到達に要した時間が出る。
450÷(90-60)=15(分)
つまり、450mの差がつくのに15分かかっていることになるので、
60×15=900(m)
≫ 練習問題の解答・解説を隠す