鶴亀算 SPI対応 解き方を解説｜無料練習問題付

 

鶴亀算の例題

＜例題＞鶴と亀が合わせて６匹いる。足の数の合計は16本であった。鶴と亀はそれぞれ何匹いるのか。※鶴は１羽、２羽と数えるがここでは匹とする。

 

例題の解答・解説

確認・・・鶴の足の数は合計２本、亀の足の数は合計４本

・全て鶴だとする
２（本）×６（匹）＝１２（本）　足の数の合計は16本なので４本足りない

・鶴を５匹、亀を１匹とする
２×５＋４×１＝１５（本）　１本足りない

・鶴を４匹、亀を２匹とする
２×４＋４×２＝１６（本)　問題に合う

・鶴を５匹、亀を３匹とする
２×５＋４×３＝２２（本）　６本オーバーする

よって答えは、鶴４匹、亀２匹

鶴亀算を面積図で解く方法

例題の鶴亀算を面積図で考えてみましょう。

長方形を２つ合わせた面積は１６です。

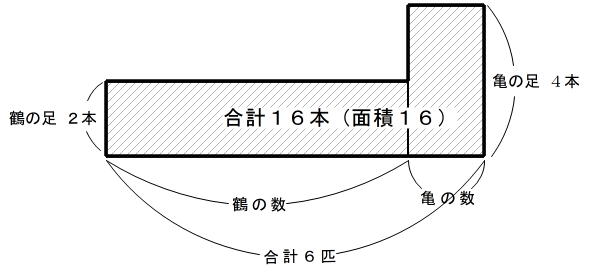
これを図のように分けると、下の長方形の面積は１２、上の長方形の面積は４です。

上の長方形の縦の長さは２なので、横の長さは４÷２＝２になります。

よって、亀の数は２匹、鶴の数は６匹－２匹＝４匹

＜別解＞
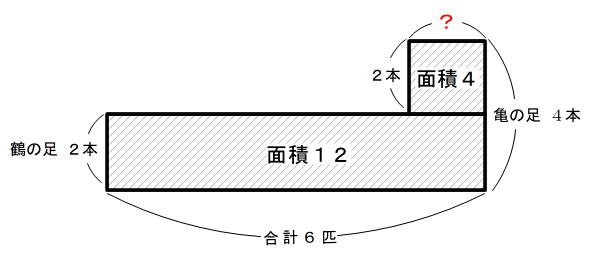
今度は、長方形を図のように足してみましょう。

長方形を足した全体の面積は２４です。

全体から赤枠の部分を引くと、２４－１６＝８になります。

面積８の縦の長さは２なので、横の長さは８÷２＝４になります。

よって、鶴の数は４匹、亀の数は６匹－４匹＝２匹

鶴亀算は、「全て鶴だったと仮定する」、あるいは、「全て亀だったと仮定する」ことで解いていく問題です。

公式にすると、次のようになります。

＜全て鶴だったと仮定する場合（足の数が少ない方を全てとする場合）＞
（合計の足数－鶴の足数×合計の頭数）÷（亀の足数－鶴の足数）＝亀の頭数
合計の頭数－亀の頭数＝鶴の頭数

＜全て亀だったと仮定する場合（足の数が多い方を全てとする場合）＞
（亀の足数×合計の頭数－合計の足数）÷（亀の足数－鶴の足数）＝鶴の頭数
合計の頭数－鶴の頭数＝亀の頭数

公式にすると、かえってややこしくなりますね。

どちらか１つの公式（計算手順）を覚えておくといいですね。

ただ、「（合計の足数－鶴の足数×合計の頭数）・・・・」なんて小学生は覚えません。

小学生は、練習問題をたくさん解くことで、自然と手が動いていきます。

一応、例題を公式にあてはめると、

（１６－２×６）÷（４－２）＝２
６－２＝４

または

（４×６－１６）÷（４－２）＝４
６－４＝２

これが基本的な鶴亀算の小学生の解き方です。

鶴亀算を方程式で解く方法

小学生の頭の柔らかさがなくなってしまった方には、方程式で解く方が理解しやすいかもしれませんね。

例題を方程式で解いてみましょう。

＜中学１年生の解き方＞

＜中学２年生の解き方＞

鶴亀算の練習問題

１．鶴と亀が合わせて１６匹いる。足の数を数えると５０本あった。亀は何匹いるのか。

Ａ　４匹　　Ｂ　５匹　　Ｃ　６匹　　Ｄ　７匹
Ｅ　８匹　　Ｆ　９匹　　Ｇ　12匹　　Ｈ　14匹

２．ニワトリと犬が合わせて２８匹いる。足の数を数えると６８本あった。ニワトリは何匹いるのか。

Ａ　10匹　　Ｂ　14匹　　Ｃ　15匹　　Ｄ　18匹
Ｅ　22匹　　Ｆ　24匹　　Ｇ　25匹　　Ｈ　26匹

３．Ａ君は、５０円の鉛筆と８０円のボールペンを合わせて１２本買って、全部で７２０円支払った。鉛筆を何本買ったのか。

Ａ　５本　　Ｂ　６本　　Ｃ　７本　　Ｄ　８本
Ｅ　10本　　Ｆ　12本　　Ｇ　14本　　Ｈ　16本

４．５０円玉と１００円玉が合わせて４７枚ある。合計金額は３９５０円である。１００円玉は何枚あるのか。

Ａ　26枚　　Ｂ　28枚　　Ｃ　31枚　　Ｄ　32枚
Ｅ　34枚　　Ｆ　35枚　　Ｇ　37枚　　Ｈ　38枚

５．６２円切手と８２円切手を合わせて２６枚買った。代金は１８９２円であった。６２円切手を何枚買ったのか。

Ａ　８枚　　Ｂ　10枚　　Ｃ　12枚　　Ｄ　14枚
Ｅ　15枚　　Ｆ　16枚　　Ｇ　18枚　　Ｈ　20枚

６．７０００円を１２人で分けることにした。ある人には６００円ずつ、その他の人にはそれより５０円少なく分けた。６００円もらった人は何人か。

Ａ　３人　　Ｂ　４人　　Ｃ　５人　　Ｄ　６人
Ｅ　７人　　Ｆ　８人　　Ｇ　９人　　Ｈ　10人

７．１００個のリンゴを１２個入る箱と８個入る箱に分けたら全部で１０箱できて、リンゴが４個余った。８個入る箱は何箱できたか。

Ａ　４箱　　Ｂ　５箱　　Ｃ　６箱　　Ｄ　７箱
Ｅ　８箱　　Ｆ　９箱　　Ｇ　10箱　　Ｈ　11箱

８．ある製品を１００個作る仕事がある。１個作ると５０円もらえるが、１個こわすごとに５０円もらえないどころか７０円支払わなければならないという。Ａ君はこの仕事を終えたときに４２８０円受け取った。Ａ君は製品を何個こわしたことになるのか。

Ａ　５個　　Ｂ　６個　　Ｃ　７個　　Ｄ　８個
Ｅ　９個　　Ｆ　10個　　Ｇ　12個　　Ｈ　15個

９．分速６５ｍで歩き、分速２４０ｍで走る人がいる。５１００ｍ離れた所に３０分間で到着するには、この人は何分間走る必要があるか。

Ａ　14分　　Ｂ　17分　　Ｃ　18分　　Ｄ　19分
Ｅ　20分　　Ｆ　22分　　Ｇ　23分　　Ｈ　24分

10．１個９０円のリンゴ、１個６０円のナシ、１個４０円のミカンを合計３２個買った。代金は１９２０円であった。また、ナシとミカンの個数は同じであった。リンゴを何個買ったのか。

Ａ　８個　　Ｂ　10個　　Ｃ　12個　　Ｄ　14個
Ｅ　16個　　Ｆ　18個　　Ｇ　20個　　Ｈ　22個

 

練習問題を紙に印刷して解きたい方のためにPDFファイルを用意しています。

ＰＤＦファイルはこちら＞＞＞turukame.pdf

鶴亀算の練習問題の解答